Math Monday: Decreasing - Part II - across a row/round

In the last installment of MATH MONDAY, I wrote about the formula for calculating decreases along a specific length. (Go back and review that, if you’d like, but we’re going to do it again in a different iteration.) We started out with a slightly more difficult example. Today, I’m going to be sharing how you evenly place decreases across a row or a round.

This is Barnstorm. The sleeves are a bit unusual.

Before we start, here’s a little bit about the sweater so we can work with the numbers: Barnstorm is a favorite of mine. I love the unique yoke patterning and ribbing. If you’re a sweater knitter, you know that typically, you need to decrease when you transition from ribbing to stockinette. Barnstorm is worked bottom up and has a split hem. The front and back hems are knitted flat in ribbing and then joined to work in the round. The rest of the body to the underarms is knit in stockinette. The sleeves have a split at the cuff, but follow the same sequence - ribbing flat, stockinette in the round to the underarm.

Sleeve detail in Barnstorm

We’ll be working on the sleeve decreases today. For this size the sleeves go from 55 sts to 38 sts. If we subtract these two numbers, we know we’ll need to decrease 17 sts across the row. We then set up our division equation, just like last time. We use 55 because this is how many stitches are starting with.

Just like last week, we solve the equation, adding 1 to the quotient and then subtracting the remainder from the divisor.

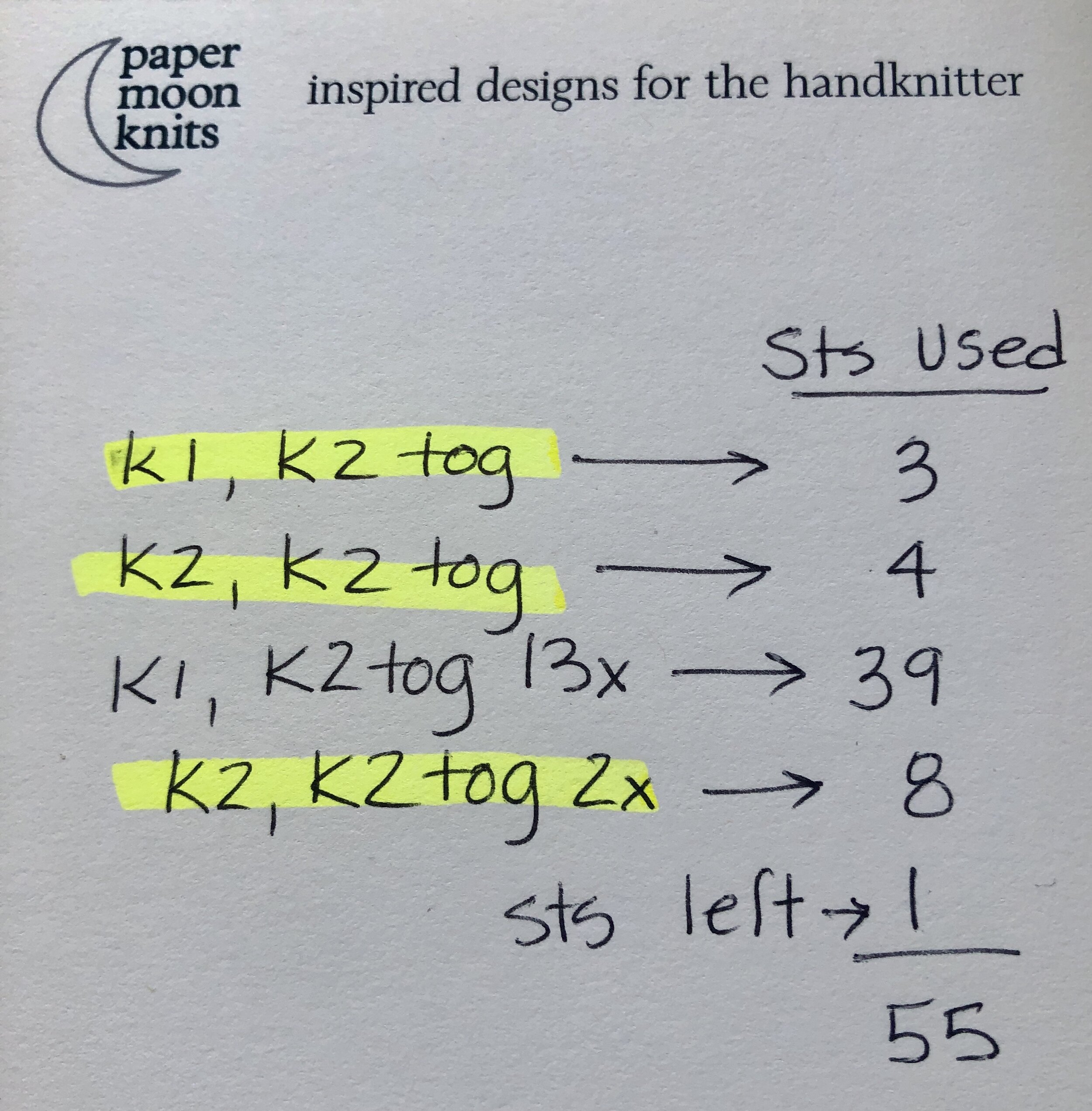
Draw the X from quotient to secondary remainder and from quotient + 1 to the remainder. We now know we have to decrease every 4th stitch 4 times and every 3rd stitch 13 times. This is a little different than last week because we are decreasing over stitches and not rows.

The first thing I want to say is that working a decrease every 4th stitch does not mean you work 4 sts and then do a decrease! It means that the decrease needs to occur so that the last worked stitch is stitch number 4.

In this case, if you’re using a k2tog decrease, you would k2, then k2tog. This would use 4 sts. If you’re working a decrease every 3rd stitch, you would k1, then k2tog. This would use 3 stitches. Remember, you only have 55 stitches to get all these decreases in.

Now for the execution. There are a number of different ways to do this. The first way is to just do the decreases as written - every 3rd stitch 13 times and every 4th stitch 4 times.

The second way would be to intersperse the every 4th between the every 3rd in a sort of even way. So every 3rd stitch 4 times, then every 4th stitch once, then every 3rd 4 times, then ever 4th once…. Four doesn’t divide evenly into 13 so you’d still have a bit of unevenness in this, and it involves math that isn’t really necessary - no one will really notice whether you’re decreasing on the 3rd or 4th stitch, except if they’re using a magnifying glass. I don’t like either of these ways because your final decrease will be on the very last stitch. Not a great idea!

Here’s what I like to do:

First I take the decrease that I’m going to do fewer times, in this case the 4th stitch every 4x, and I divide that in half. I’ll do this decrease 2x at the beginning of the row and then 2x at the end with the 13 decreases every 3rd stitch in between. Before I get started though, I want to make sure I don’t end up with a decrease on the very last stitch, so I’ll split that first decrease in half. Instead of doing it at the 4th stitch, I’ll do it at the 2nd. This works when the first decrease is more than 2 stitches because if I do this, then I’ll have to start out with a decrease at the very beginning of the row (remember, the last stitch of the decrease will have to be on stitch 2 which means I’ll start out with a k2tog) - also not a good idea.

So what I’ll do in this case is k1, k2tog as my very first 4 stitch decrease - (I know it’s really only 3 stitches). Then I’ll do k2, k2tog (my second 4-stitch decrease). Then I’ll do k1, k2tog 13 times. Then I’ll do k2, k2tog 2 times (as my last two 4-stitch decreases and I have 1 stitch left over. The beginning and the end of the row have the same number of stitches!

The proof is in the math! The highlighted lines show the 4-stitch decreases done 4 times.

The beauty of this method is that it works the same way for knitting flat as knitting in the round. The one stitch at the beginning and end of the round equal 2 stitches between the k2togs.

Math Monday: Decreasing - Part I - along the length

This is Enracine, a cool linen top from 2020.

Long division. Do you remember?

This Monday, I’ll be teaching you how to use long division to calculate decreases —one that is used to taper a sleeve or the body of a sweater. Next week we’ll use it for decreases along a row or round.

Sleeve schematic for Enracine

There are 3 measurements you’ll need to calculate this type of decrease: a starting point (E), an ending point (G) and the length over which you’d like the decreases to occur (F). Of course, you’ll also need your stitch and row gauge.

In the sample size, the starting point circumference was 13” [33cm]. If we multiply this number by our stitch gauge of 4.75 sts/inch, we know that our starting point stitch count is 62 sts - rounded to the nearest even number. Our ending point circumference is 9.5” [24cm]. If we multiply this number by by our stitch gauge, we know that our ending stitch count is 46 sts - again, rounded to the nearest even number. By the way, it doesn’t have to be even, but both numbers have to be the same - both odd or both even.

The difference between 62 and 46 is 16 sts, and we need to do these decreases in sets, one on each side of the “seam line” of the sleeve. This means there are 8 sets of decrease points along the sleeve for this size (16 divided by 2).

The decreases occur at the inside of the sleeve.

Now for this design, I wanted three-quarter sleeves, so the length of the sleeve for all sizes is 9.5” [24cm]. They seem shorter than normal because this design was a drop shoulder. We’ll discuss that another time. The row gauge is 8.25 rounds per inch as the sleeves are knitted in the round. It works the same way for pieces knitted flat. Decreases shouldn’t start at the first round of the piece and shouldn’t end on the last round either, so the rule of thumb is usually to leave 1” [2.5cm] at the top and bottom before the first and after the last decrease. This reduces our length by 2” [5cm]. Now we only have 7.5” [19cm] to work with.

Multiply 7.5” by our row gauge of 8.25 gives us approximately 60 rounds to work with.

Now comes the long division:

Follow the steps beginning at the top left.

Only 1 more step and we’re done!

Draw arrows that cross from the quotient and the quotient + 1 to the remainder and the difference between the divisor and remainder. This tells you that to get evenly spaced decreases, you work a set of decreases every 7th round 4 times, and every 8th round 4 times. You can alternate these - every 7th, then every 8th, then every 7th…. - or you can just work decreases every 8th round 4 times, then every 7th round 4 times.

You can also do a little math check if you want to prove to yourself it works:

Multiply number of rounds to decrease by number of times to check your answer! IT WORKS !

Now isn’t math awesome?